
前言
不开心,不想说话……让我们直接进入这段有趣的学习之旅吧,试试两个月,甚至更短的时间内解决掉这门又臭又长的课程。
Bits, Bytes, and Integers
Representation information as bits
Everything is bits
Each bit is 0 or 1
By encoding/interpreting sets of bits in various ways
- Computers determine what to do (instructions)
- … and represent and manipulate numbers, sets, strings, etc…
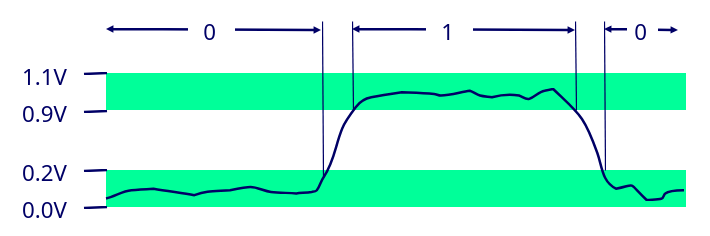
Why bits? Electronic Implementation
- Easy to store with bitsable elements
- Reliably transmitted on noisy and inaccurate wires
- Easy to indicate low level/high level
Bit-level manipulations
Representing & Manipulating Sets
Representation
We can use bits to determine whether an element belongs to a set. Say each bit have index, which corresponds to a number from zero. If a bit is set to 1, it means the corresponding index (i.e., the element) is in the set. Otherwise, its not.
In a more mathematical representation way:
- Width bit vector represents subsets subsets of
- if
Sets Operations
&is related to Intersection|is related to Union~is related to Complement^is related to Symmetric difference
Shift Operations
-
Left Shift:
x << y- Shift bit-vector
xleftypositions- Throw away extra bits on left
- Fill with 0’s on right
- Shift bit-vector
-
Right Shift:
x >> y- Shift bit-vector
xrightypositions- Throw away extra bits on right
- Logical shift
- Fill with 0’s on left
- Arithmetic shift
- Replicate most significant bit on left
- Shift bit-vector
Undefined Behaviour
- Shift amount 0
- Shift amount word size
- Left shift a signed value
Integers
Representation: unsigned and signed
Unsigned
Two’s Complement
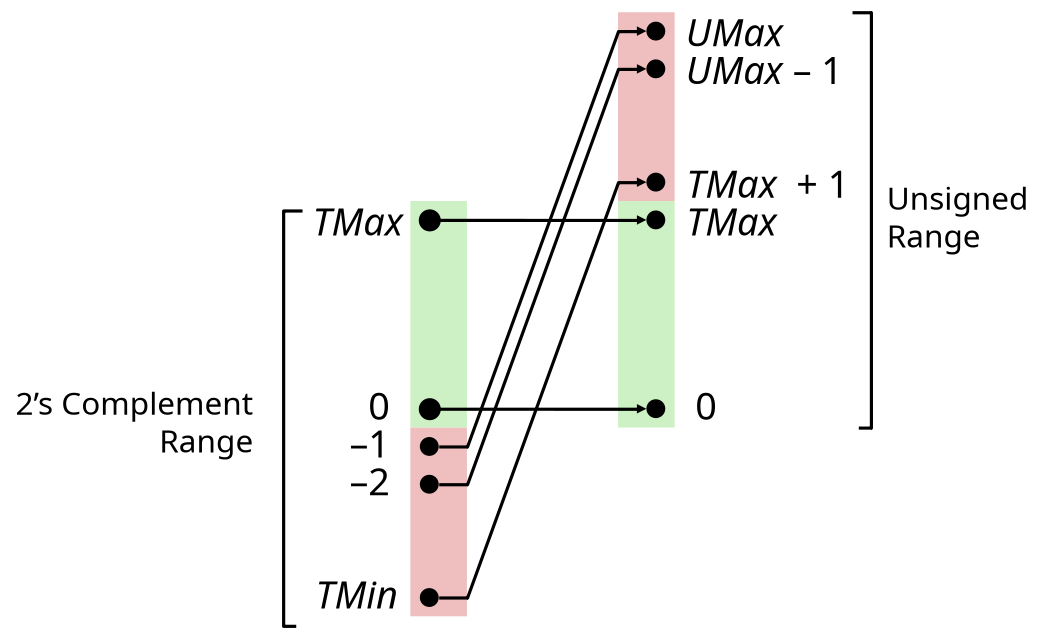
Invert mappings
Numeric Ranges
-
Unsigned Values
-
Two’s Complement Values
TIPIn C, these ranges are declared in
limits.h. e.g.,ULONG_MAX,LONG_MAX,LONG_MIN. Values are platform specific.
Observations
-
- Asymmetric range (Every positive value can be represented as a negative value, but cannot be represented as a positive value)
Difference between Unsigned & Signed Numeric Values
The difference between Unsigned & Signed Numeric Values is .
For example, if you want convert a unsigned numeric value to its signed form, just use this value minus , or if you want convert a signed numeric value to its unsigned form, you plus .
Conversion, casting
Mappings between unsigned and two’s complement numbers keep bit representations and reinterpret.
For example, casting a signed value to its unsigned form, the most significant bit from large negative weight becomes to large positive weight and vice versa.
Constants
- By default are considered to be signed integers.
- Unsigned if have “U” as suffix
Casting
- Explicit casting between signed & unsigned same as and
- Implicit casting also occurs via assignments and procedure call (assignments will casting to lhs’s type)
Expression Evaluation
- If there is a mix of unsigned and signed in single expression, signed values implicitly cast to unsigned
- Including comparison operations
<,>,==,<=,>
| Constants 1 | Constants 2 | Relation | Evaluation |
|---|---|---|---|
0 | 0U | == | unsigned |
-1 | 0 | < | signed |
-1 | 0U | > | unsigned |
2147483647 | -2147483647-1 | > | signed |
2147483647U | -2147483647-1 | < | unsigned |
-1 | -2 | > | signed |
(unsigned)-1 | -2 | > | unsigned |
2147483647 | 2147483648U | < | unsigned |
2147483647 | (int)2147483648U | > | signed |
Expanding, truncating
Sign Extension
- Make copies of sign bit
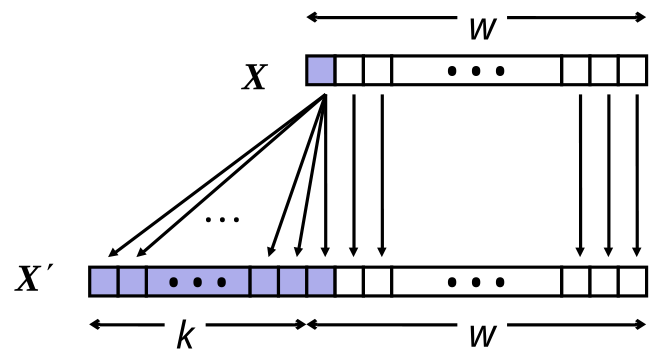
WARNINGConverting from smaller to larger integer data type. C automatically performs sign extension.
Expanding (e.g., short int to int)
- Unsigned: zeros added
- Signed: sign extension
- Both yield expected result
Truncating (e.g., unsigned to unsigned short)
- Unsigned/signed: bits are truncated
- Result reinterpreted
- Unsigned: mod operation
- Signed: similar to mod
- For small numbers yields expected behavior
Addition, negation, multiplication, shifting
Unsigned Addition
- Standard Addition Function
- Ignore carry output
- Implements Modular Arithmetic
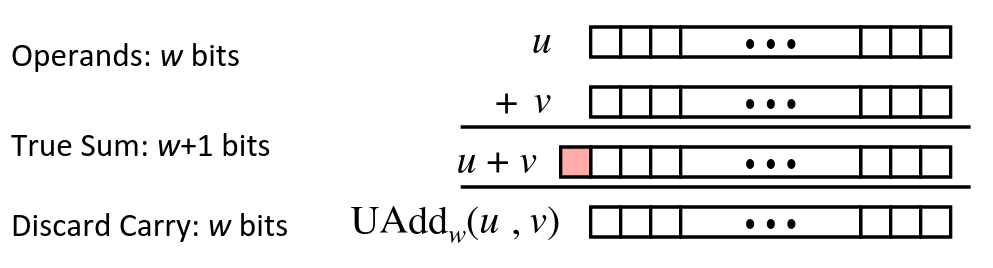
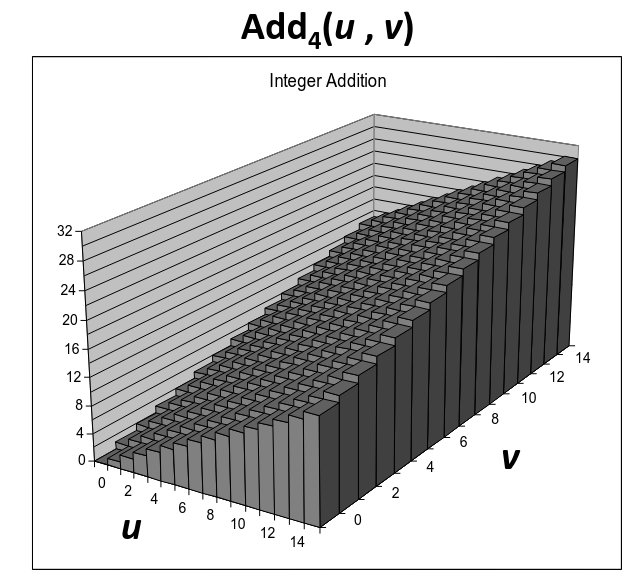
Visualizing (Mathematical) Integer Addition
- Integer Addition
- 4-bit integers
- Compute true sum
- Values increase linearly with and
- Forms planar surface
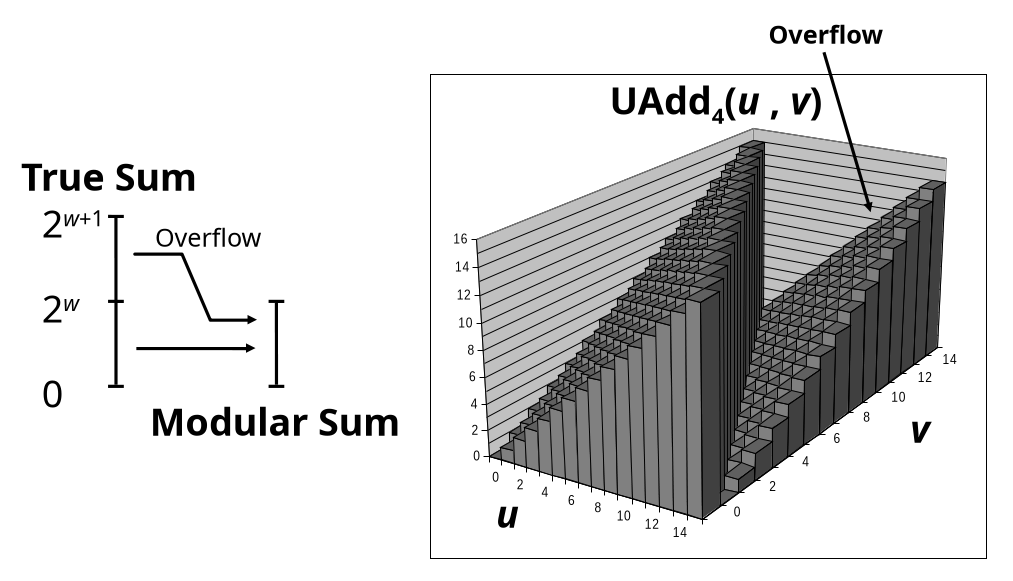
Visualizing Unsigned Addition
- Wraps Around
- If true sum
- At most once
Two’s Complement Addition
- and have Identical Bit-level Behaviour
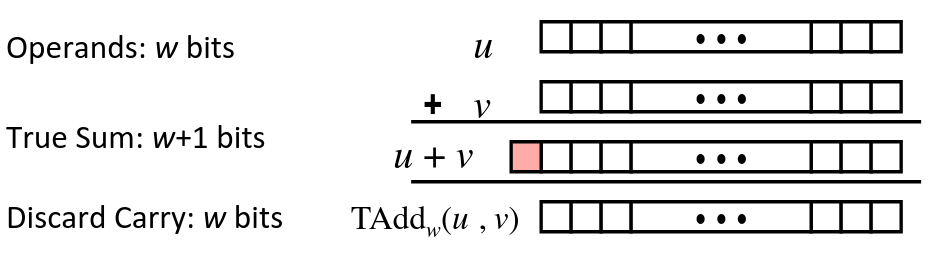
Signed vs. unsigned addition in C:
int s, t, u, v;
s = (int)((unsigned)u + (unsigned)v);t = u + v;
// will give s == tTAdd Overflow

- Functionality
- True sum requires bits
- Drop off MSB
- Treat remaining bits as two’s complement integer
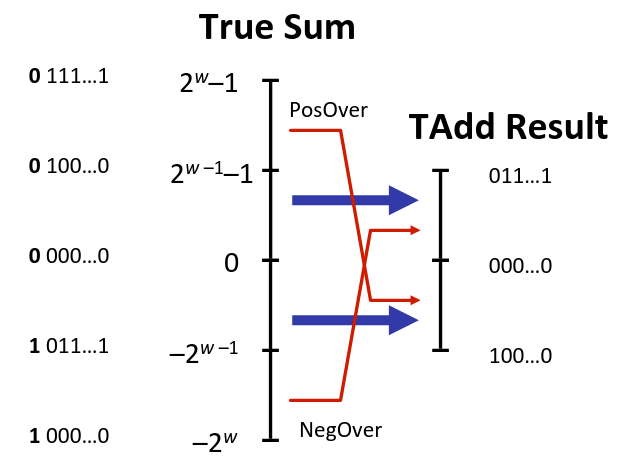
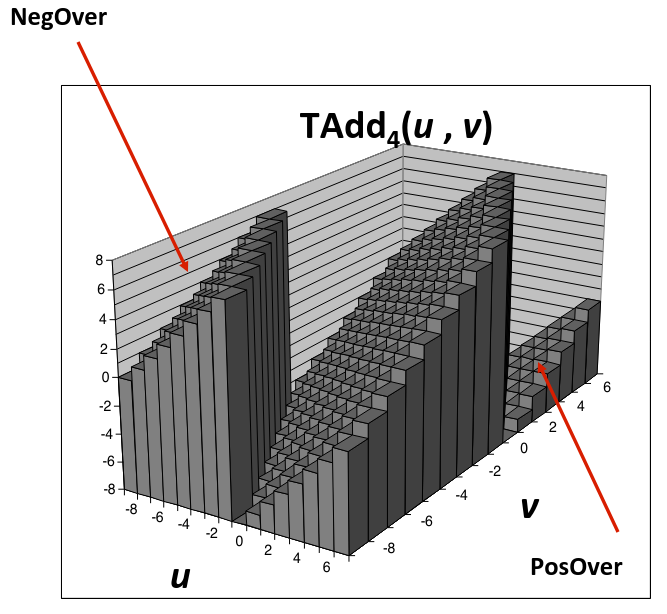
Visualizing Two’s Complement Addition
-
Values
- 4-bit two’s comp.
- Range from to
-
Wraps Around
- If sum
- Becomes negative
- At most once
- If sum
- Becomes positive
- At most once
- If sum
Multiplication
- Goal: Computing Product of -bit numbers
- Either signed or unsigned
- But, exact results can be bigger than bits
- Unsigned: up to bits
- Result range:
- Two’s complement min (negative): Up to bits
- Result range:
- Two’s complement max (positive): Up to bits, but only for
- Result range:
- Unsigned: up to bits
- So, maintaining exact results…
- would need to keep expanding word size with each product computed (exhaust memory faster)
- is done in software, if needed
- e.g., by “arbitrary precision” arithmetic packages
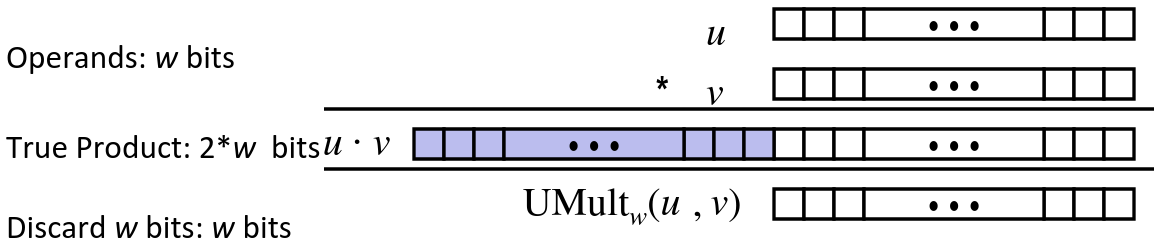
Unsigned Multiplication in C
- Standard Multiplication Function
- Ignore high order bits
- Implements Modular Arithmetic
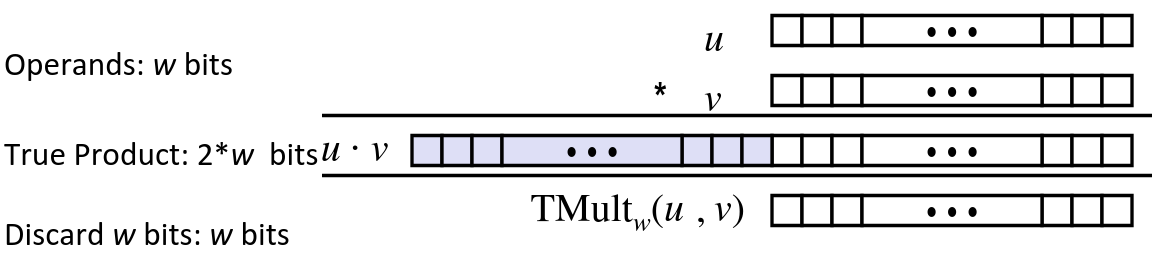
Signed Multiplication in C
- Standard Multiplication Function
- Ignore high order bits
- Some of which are different for signed vs. unsigned multiplication
- Lower bits are the same
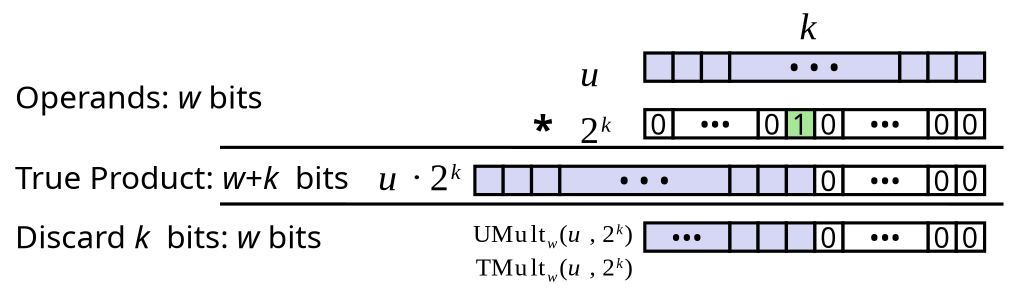
Power-of-2 Multiply with Shift
- Operation
u << kgives (basically increases each bits weight)- Both signed and unsigned
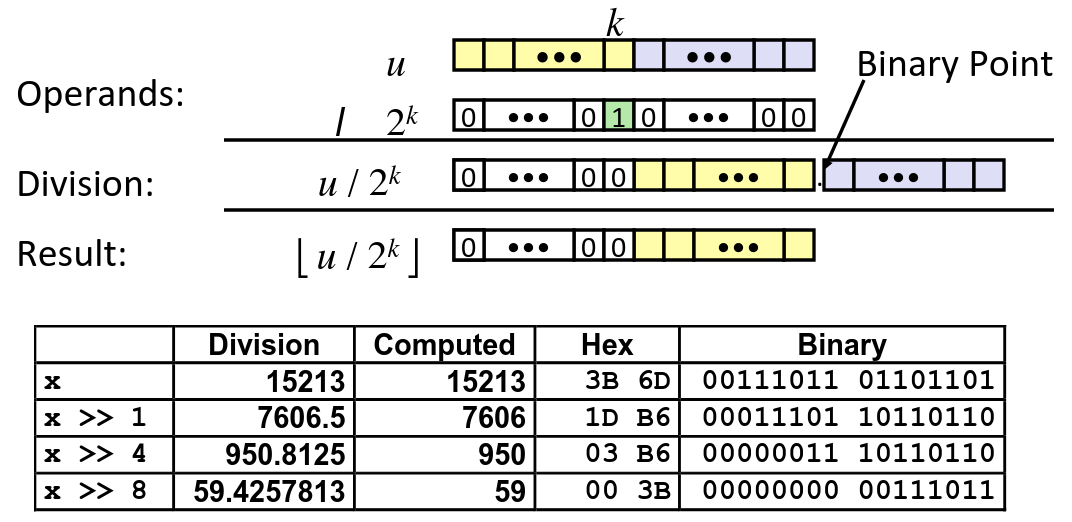
Unsigned Power-of-2 Divide with Shift
- Quotient of Unsigned by Power of 2
u >> kgives- Uses logical shift
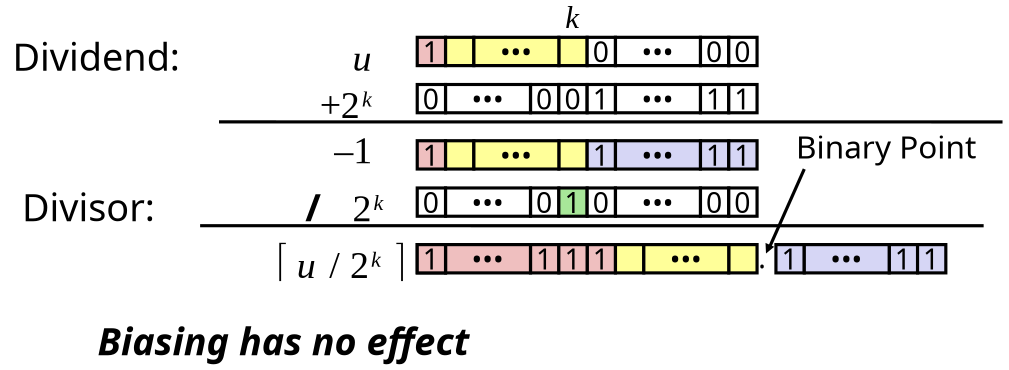
Signed Power-of-2 Divide with Shift
- Quotient of Signed by Power of 2
- Uses arithmetic shift
- Want (Round toward 0)
- Compute as
- In C:
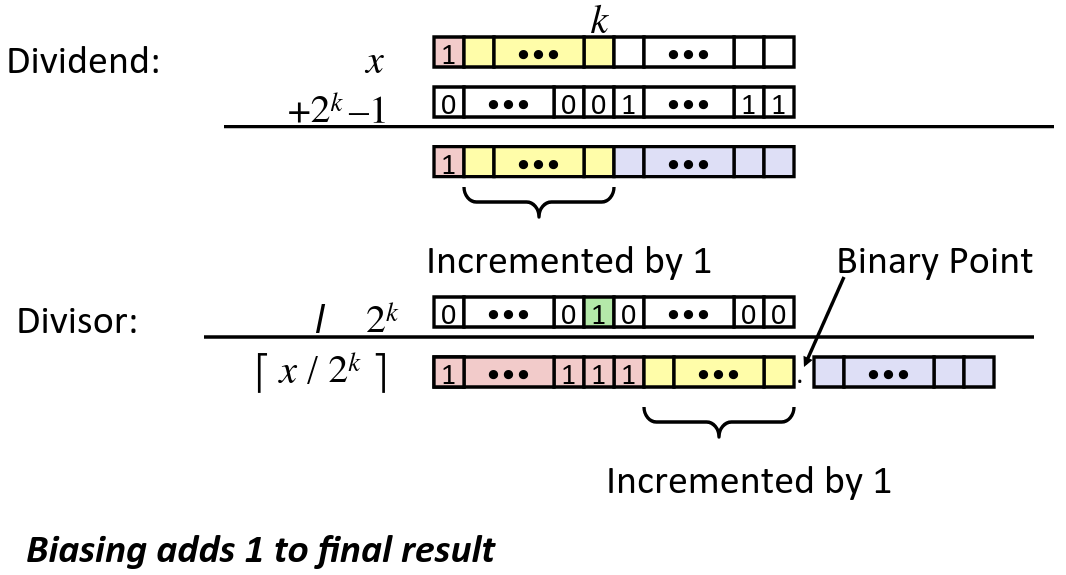
(x + (1 << k) - 1) >> k - Biases dividend toward 0
- In C:
Case 1: No rounding
Case 2: Rounding
Handy tricks
If you want convert a value to its negative form by hand or in mind, either unsigned or signed.
Just do:
When Should I Use Unsigned?
Don’t use without understanding implications!
- Do use when performing modular arithmetic
- Multiplication arithmetic
- Do use when using bits to represent sets
- Logical right shift, no sign extension
Representation in memory, pointers, strings
Byte-Oriented Memory Organization
- Programs refer to data by address
- Conceptually, envision it as a very large array of bytes
- In reality, it’s not, but can think of it that way
- An address is like an index into that array
- and, a pointer variable stores an address
- Conceptually, envision it as a very large array of bytes
- System provides private address spaces to each “process”
- So, a program can clobber its own data, but not that of others
Machine Words
- Any given computer has a “Word Size”
- Nominal size of integer-valued data
- and of addresses
- Until recently, most machines used 32 bits (4 bytes) as word size
- Limits addresses to 4GB ( bytes)
- Increasingly, machines have 64‐bit word size
- Potentially, could have 18 EB (exabytes) of addressable memory
- That’s bytes
- Machines still support multiple data formats
- Fractions or multiples of word size
- Always integral number of bytes
- Nominal size of integer-valued data
Word‐Oriented Memory Organization
- Addresses Specify Byte Locations
- Address of first byte in word
- Addresses of successive words differ by 4 (32‐bit) or 8 (64‐bit)
Byte Ordering
- Big Endian: Sun, PPC Mac, Internet
- Least significant byte has highest address
- Little Endian: x86, ARM processors running Android, iOS, and Windows
- Least significant byte has lowest address
Representation Strings
In C, either little endian or big endian machine, strings in memory represented in the same way, because a string is essentially an array of characters ends with \x00, each character is one byte encoded in ASCII format and single byte (character) do not obey the byte ordering rule.
Floating Point
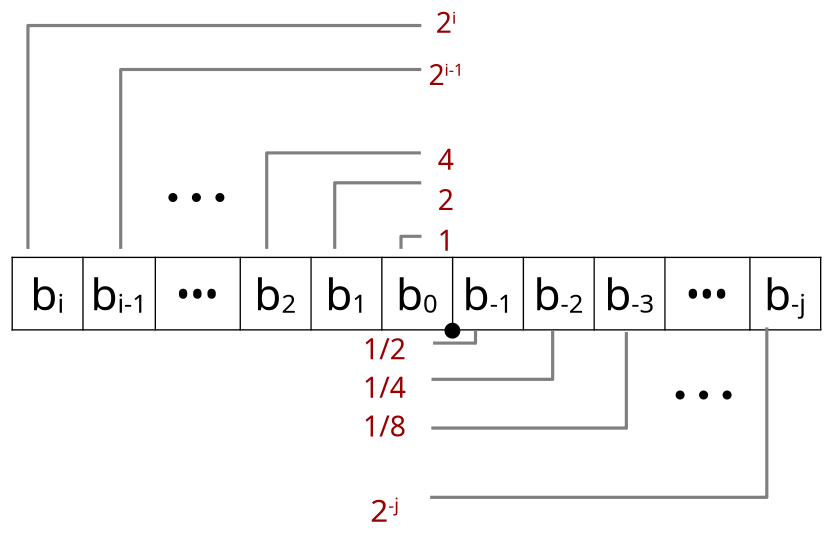
Background: Fractional binary numbers
Representing
- Bits to right of “binary point” represent fractional powers of 2
- Represents rational number:
| Value | Representation |
|---|---|
Observations
- Divide by 2 by shifting right (unsigned)
- Multiply by 2 by shifting left
- Numbers of form are just below
- Use notation − ( depends on how many bits you have to the right of the binary point. If it gets smaller the more, the more of those bits you have there, and it gets closer to )
Limitation 1
- Can only exactly represent numbers of the form
- Other rational numbers have repeating bit representations, but cause computer system can only hold a finite number of bits, so
| Value | Representation |
|---|---|
Limitation 2
- Just one setting of binary point within the bits
- Limited range of numbers (very small values? very large? we have to move the binary point to represent sort of wide as wide a range as possible with as much precision given the number of bits)
Definition: IEEE Floating Point Standard
IEEE Standard 754
Established in 1985 as uniform standard for floating point arithmetic. Before that, many idiosyncratic formats.
Although it provided nice standards for rounding, overflow, underflow… It is hard to make fast in hardware (Numerical analysts predominated over hardware designers in defining standard)
Floating Point Representation
Numerical form:
- Sign bit
sdetermines whether number is negative or positive - Significand
M (Mantissa)normally a fractional value in range - Exponent
Eweights value by power of two
Encoding
- MSB
sis sign bits expfield encodesE(but is not equal toE)fracfield encodesM(but is not equal toM)

Normalized Values
When: and
- Exponent coded as a biased value:
- is unsigned value of exp field
- , where is number of exponent bits
- Single precision: (, )
- Double precision: (, )
- Significand coded with implied leading :
- is bits of frac field
- Minimum when
- Maximum when
- Get extra leading bit for “free”
Normalized Encoding Example
-
Value:
float F = 15213.0; -
Significand
-
Exponent
So the result would be:

# manually calculate((-1)**0)*(1+1/2+1/4+1/16+1/32+1/128+1/256+1/1024+1/2048+1/8192)*(2**13) == 15213.0
# by struct packageimport struct
bits = 0b01000110011011011011010000000000f = struct.unpack("f", struct.pack("I", bits))[0]
print(f)Denormalized Values
- Condition:
- Exponent value:
- Significand coded with implied leading :
- is bits of frac field
- Cases
-
- Represents zero value
- Note distinct values: and
-
- Numbers closet to
- Equispaced
-
Special Values
-
Condition:
-
Case:
- Represents value
- Operation that overflows
- Both positive and negative
- E.g.,
-
Case:
- Not-a-Number (NaN)
- Represents case when no numeric value can be determined
- E.g.,
Visualization: Floating Point Encodings

Example and properties
Tiny Floating Point Example
Think about this 8-bit Floating Point Representation below, it obeying the same general form as IEEE Format:
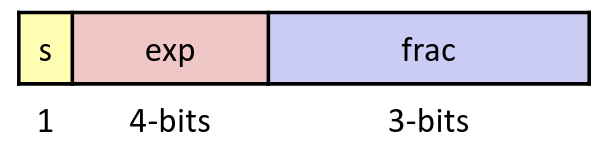
Dynamic Range (Positive Only)
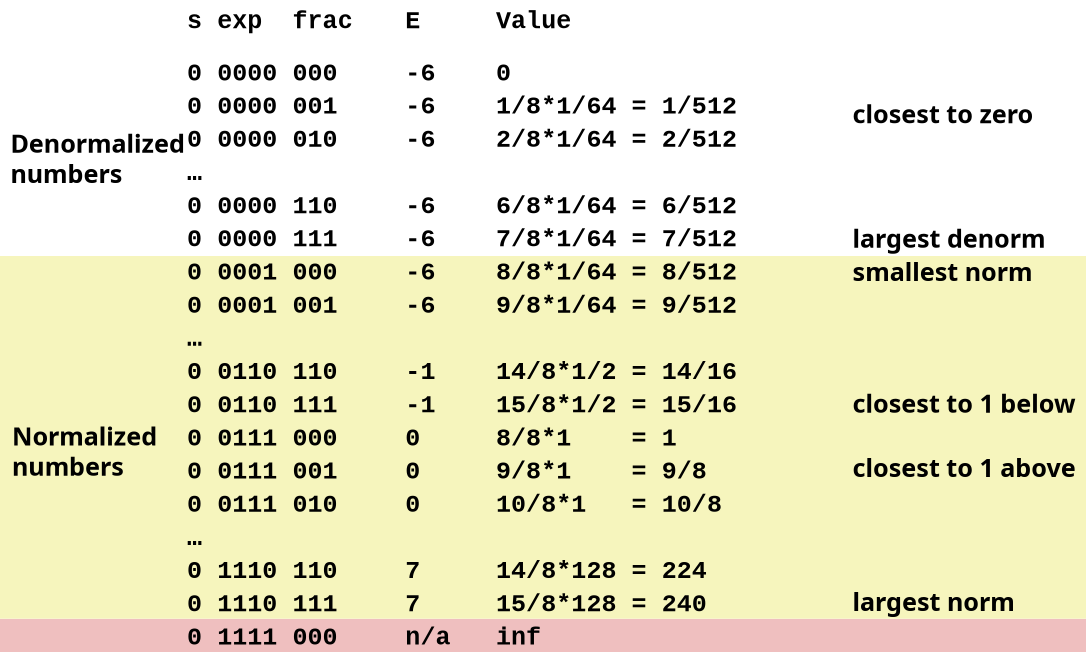
Distribution of Values
Still think about our tiny example, notice how the distribution gets denser toward zero.
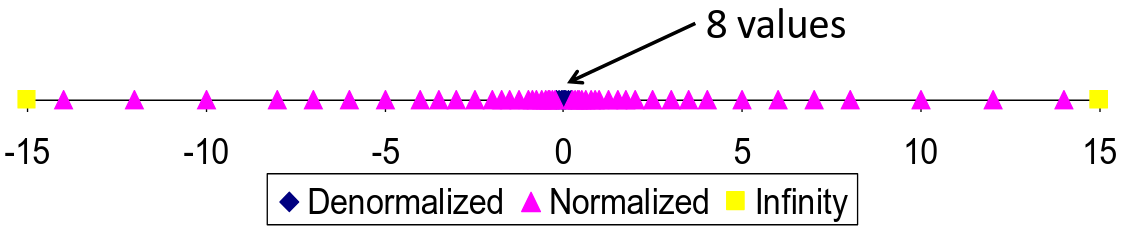
Here is a scaled close-up view:

Special Properties of the IEEE Encoding
- FP Zero Same as Integer Zero
- All bits = 0
- Can (Almost) Use Unsigned Integer Comparison
- Must first compare sign bits
- Must consider
- NaNs problematic
- What should comparison yield?
- Otherwise OK
- Denormalized vs. Normalized
- Normalized vs. Infinity
Rounding, addition, multiplication
Floating Point Operations: Basic Idea
Basic idea
- First compute exact result
- Make it fit into desired precision
- Possibly overflow if exponent too large
- Possibly round to fit into frac
Rounding
Rounding Modes (illustrate with $ rounding)
| $1.40 | $1.60 | $1.50 | $2.50 | -$1.50 | |
|---|---|---|---|---|---|
| Towards Zero | $1 | $1 | $1 | $2 | -$1 |
| Round Down () | $1 | $1 | $1 | $2 | -$2 |
| Round Up () | $2 | $2 | $2 | $3 | -$1 |
| Nearest Even (default) | $1 | $2 | $2 | $2 | -$2 |
Round to EvenIt means, if you have a value that’s less than half way then you round down, if more than half way, round up. When you have something that’s exactly half way, then what you do is round towards the nearest even number.
Closer Look at Round-To-Even
Default Rounding Mode
- Hard to get any other kind without dropping into assembly
- All others are statistically biased
- Sum of set of positive numbers will consistently be over or underestimated
Applying to Other Decimal Places / Bit Positions
- When exactly half way between two possible values
- Round so that least significant digit is even
E.g., round to nearest hundredth:
| Value | Rounded | |
|---|---|---|
| 7.8949999 | 7.89 | Less than half way |
| 7.8950001 | 7.90 | Greater than half way |
| 7.8950000 | 7.90 | Half way (round up) |
| 7.8850000 | 7.88 | Half way (rond down) |
